conics.15887.pts
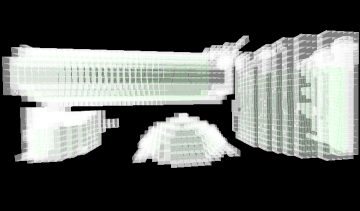
Figure 1: f(p) at marching cubes	Figure 2: resultant triangles
mechpart.4102.pts
Figure 3: f(p) at marching cubes	Figure 4: resultant triangles

1. For each cube that intersects the signed distance function, find the triangles formed by the cube/signed distance function intersection:
   • Using an STL bitset<8> fb as the bit code for the cube, where each bit represents whether each vertex is above the surface (f(p_i) is positive) or below it (f(p_i) is negative), such that for each k^th vertex the bit value is:

     fb[k] = f(pi) >= 0.0 ? 1 : 0;

     find the set of intersected edges from a lookup table that accepts the bitset as the lookup index, e.g.,

     index = (int)fb.to_ulong();
cubeEdges = intersections[index];

     where each such record is represented by a 3-tuple of vertex pair indeces and the next index into the intersections list (with -1 indicating no further records), e.g.,

     int intersections[484][7] = {
    {-1,-1,-1,-1,-1,-1,-1},
    {0,1,0,4,0,2,-1},
    {1,5,1,0,1,3,-1},
    {0,2,1,3,0,4,262},
    {2,3,2,0,2,6,-1},
    {0,1,2,6,2,3,264},
...
};

     see marchingCube.h and marchingCube.cpp.
   • For each of the three edges (three pairs of vertex indeces i, j), calculate the point of intersection along each edge:
     • With each pair of verteces v_i and v_j, let t = -f(v_i) / (f(v_j) - f(v_i)) (remember that f(p_i) is stored at each vertex point).
     • Return the interpolated intersection point p = v_i + t (v_j - v_i).
   • Add computed triangle to edge of triangles, calculating the triangle normal as you do so by letting u = p₁ - p₀, v = p₂ - p₀, and n = cross(u,v) and normalizing.
   • Check to see if there is another 3-tuple intersection record to process (some cubes may produce 4 triangles).
2. You now should have a list of triangles (see Figure 2).
3. Output your triangle data to a plain text file in the following format:
   tri[0].n
   tri[0].p₀
   tri[0].p₁
   tri[0].p₂
   ...
   tri[n-1].n
   tri[n-1].p₀
   tri[n-1].p₁
   tri[n-1].p₂
   where each of the triangles's verteces, tri[i].p_j is a 3D point and tri[i].n is the triangle's (3D) surface normal.
4. Sample output can be found here: conics.15887.tris, mechpart.4102.tris.
5. You can view your output with the kdtree program. Load your field file to view it. You can then check the "cubes" checkbox in the View menu to see the marching cubes with signed distance at each vertex. The program was last compiled on a Linux PC running Fedora Core 3 with g++ v3.4.3 and so should run on most of the FX net Linux boxes (but not on the Suns).
   Usage:
   • left mouse: move camera in xy-plane (up/down, left/right)
   • scroll mouse: truck in and out (along camera's view-axis)
   • CTRL-left mouse: yaw/pitch camera
   • CTRL-scroll mouse: roll camera

1. README file containing assignment and solution descriptions, e.g., program design, description of algorithm, etc., if appropriate.
2. INSTALL file containing any specific compliation quirks peculiar to your program, e.g.,
   Compilation: make.
3. USAGE file containing any specific usage quirks peculiar to your program, e.g.,
   Usage: ./phase4 < conics.15887.pts where ./phase4 is the executable and conics.15887.pts is the input.
4. src/ directory with source code.