Lab 1: Binary Search Trees
Trees
- Definition: A tree is a collection of nodes. The collection consists
of one node is distinguished as the root and zero or more subtrees whose roots are
connected by a directed edge to the root (p. 113)
- Terminology pp. 113-114
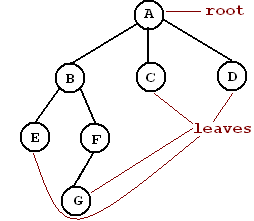
- Root: a distinguished node from which all subtrees proceed.
- Edge: A line joining two nodes in a tree. The line is directed;
that is, it can be traveled in only one direction (down). e.g. There is an
edge from A to B, but not from B to A.
- Child: A node n2 is a child of node
n1 if there is an edge from n1 to
n2. e.g. F is a child of B. B is the Parent of F.
- Siblings: Two nodes are siblings if they share the same parent.
e.g. B, C, and D are siblings, as are E and F.
- Leaf: a leaf is a node with no children.
- Path: a path from node n1 to
nk is defined as a sequence of nodes n1,
n2, . . ., nk such that ni is the parent
of ni+1 for 1 <= i < k.
e.g. There is a path of length 3 from A to G: ABFG. There is NOT a
path from C to B.
- Ancestor a node n1 is an ancestor to node
n2 if there is a path from n1 to
n2. If this is the case, then n2 is a
descendent of n1.
- Depth: a node n1's depth is the length of the path (number of edges)
from the root to n1. e.g. The depth of E is 2.
- Height: The height of a tree is the longest path from the root to a
leaf. e.g. The height of this tree is 3.
Binary Search Trees pp. 124-130
- Definition: A binary tree (a tree in which no node can have more than
two children) with the following property:
for every node n in the tree, the values of all nodes in n's left subtree are
smaller than n, and the values of the nodes in n's right subtree
are greater than n.
- Uses: Quick searches of nodes (O log2N) and sorting of data.
- Building a tree: consider adding the following values to a tree: 3 9 2 8 4 5 10 1
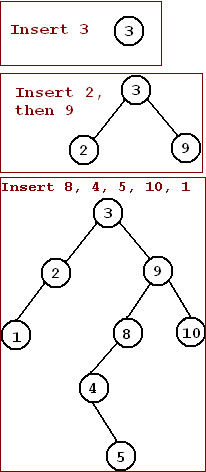
- Insert 3: Since the tree is empty, 3 becomes the root.
- Insert 9: Compare 9 to 3. 9 > 3. Insert 9 to the right of 3.
- Insert 2: Compare 2 to 3. 2 < 3. Insert 2 to the left of 3.
- Insert 8: Compare 8 to 3. 8 > 3. Insert 8 to the right of 3.
Compare 8 to 9. 8 < 9. Insert 8 to the left of 9.
- Insert 4: Compare 4 to 3. 4 > 3. Insert 4 to the right of 3.
Compare 4 to 9. 4 < 9. Insert 4 to the left of 9.
Compare 4 to 8. 4 < 8. Insert 4 to the left of 8.
- Insert 5: Compare 5 to 3. 5 > 3. Insert 5 to the right of 3.
Compare 5 to 9. 5 < 9. Insert 5 to the left of 9.
Compare 5 to 8. 5 < 8. Insert 5 to the left of 8.
Compare 5 to 4. 5 > 4. Insert 5 to the right of 4.
- Insert 10: Compare 10 to 3. 10 > 3. Insert 10 to the right of 3.
Compare 10 to 9. 10 > 9. Insert 10 to the right of 9.
- Insert 1: Compare 1 to 3. 1 < 3. Insert 1 to the left of 3.
Compare 1 to 2. 1 < 2. Insert 1 to the left of 2.
- Implementation
- The Binary Search Tree class stores a link to the root node.
- The root node has a data value, a link to a left child, and
a link to a right child.
- Similarly, every other node in the tree has data, a left link, and a right link.
If the node does not have a child, the link is NULL.
Lab: Simple Binary Search Tree
- Create a BinaryNode class with the following header:
class BinaryNode {
private:
int data;
BinaryNode *left, *right;
public:
BinaryNode ();
// default constructor: data set to zero
BinaryNode (int d); // conversion constructor
BinaryNode (int d, BinaryNode *l, BinaryNode *r);
friend class BinarySearchTree; // allows access to private members
};
- Create a BinarySearchTree class with the following header:
class BinarySearchTree {
private:
BinaryNode *root;
void makeEmpty (BinaryNode * &node);
void insert (int value, BinaryNode * &node);
void printTree (const BinaryNode *node, ostream &out);
public:
BinarySearchTree (); // initialize the root to NULL
~BinarySearchTree (); // calls "makeEmpty"
bool isEmpty(); // check if the root is NULL
void makeEmpty (); // calls internal "makeEmpty" on the root
void insert (int value); // calls internal "insert" on the root
void printTree (ostream &out); // calls internal "printTree"
};
Explanation of Notations
- Recursive functions: private
makeEmpty,
insert, and printTree are recursive methods.
That is, in order to make a node empty, you must first make its subtrees empty. Thus,
makeEmpty is called recursively on the subtrees first before deleting the current node.
Similarly, insert is called recursively on subtrees to find the correct insertion point.
In order to start the recursion, the public methods makeEmpty,
insert, and printTree call the private versions with the
root as the starting point.
- References to pointers:
insert uses a reference to a pointer. The reason that we
need to be able to change where the node points when we insert. (e.g., if node points to NULL,
we need to change it to point to the new BinaryNode we are inserting.) We could
use a pointer to a pointer; however, C++'s references allow simpler
notation.
- private
makeEmpty:
- This internal method removes the node passed in and its descendents.
- Before deleting the node, we call
makeEmpty on its children.
- After the children have been made empty, we
delete this node a point it to NULL. Pointing the node to to NULL is effective outside of
the method call because the node passed in as a reference to a pointer.
- private
insert: 3 insertion cases
- If the node we're inserting to is NULL, insert this value as that node.
- Otherwise, if this value is < the value at the current node, call insert to the
left child.
- Otherwise, insert to the right child.
- private
printTree: (inorder printing)
- Call printTree on the left child.
- Output the value of
node.
- Call printTree on the right child.
- Test code with the following main function:
int main (int argc, char *argv[]) {
BinarySearchTree tree;
if (argc < 2) {
cerr << "USAGE: " << argv[0]
<< " list of numbers to insert " << endl;
return EXIT_FAILURE;
}
for (int i=1; i < argc; ++i) {
tree.insert (atoi(argv[i]));
}
tree.printTree(cout); // Prints inputted numbers in sorted order
return EXIT_SUCCESS;
}
- Turn in your code and a Makefile to create
a.out.
Use sendlab.212.302 1 *.cpp *.h Makefile
|

