Lab 3: Templates and Matrices
Templates pp. 30-32, 567-570
- Motivation: In last week's lab, you wrote a Binary Search Tree for integers. If you wanted to use strings instead, you would have to write a different BST for strings. A better solution is to write a generic BST that can store any data that can be sorted by operator<. These generic classes are called template classes.
- Implementation:
- Template classes are defined completely with the generic data specified as templated. (e.g. in the BNode class, you could name the template type to be "T" and then have the data be of type T.)
- Since template classes are not really complete classes, they are defined completely in the header.
- When you compile a template, you may not detect all the existing errors until you compile it with a driver class. This anomaly is from the fact that until the template class is given a type, some of the compilation problems are not visible.
- Template classes are a confusing concept, even to the compiler. Because of this, you may find that the template definitions seem a bit redundant. However, the compiler needs a lot of help to stay on track with templates.
Template Example
// forward declarations (required by the compiler)
template <typename T> class BNode;
template <typename T> std::ostream &operator<< (std::ostream &out, const BNode<T> &node);
template <typename T>
class BNode {
public:
T data;
BNode<T> *left, *right;
BNode (const T &d, BNode *l, BNode *r);
BNode (const BNode &node);
bool operator<(const T &value) const;
friend std::ostream &(::operator<< <>)(std::ostream &out, const BNode &node);
};
template<typename T>
BNode<T>::BNode (const T &d, BNode *l, BNode *r) : data (d), left (l), right (r) {
}
template<typename T>
bool BNode<T>::operator<(const T &value) const {
return data < value;
}
template<typename T>
std::ostream &operator<<(std::ostream &out, const BNode<T> &node) {
if (NULL != node.left) {
out << *node.left;
}
out << node.data << std::endl;
if (NULL != node.right) {
out << *node.right;
}
return out;
}
// In the user program, you must specify what data type or types you wish the
// the template class to use. The specification must be made for the class and
// any friend functions
template class BNode<int>;
template std::ostream &operator<< (std::ostream &out, const BNode<int> &node);
template class BNode<string>;
template std::ostream &operator<< (std::ostream &out, const BNode<string> &node);
Matrix Class
- A matrix is an array of arrays or a two dimensional array.
- Our matrix class will be templated for later use in this course.
- Our internal storage of the 2D array will involve a
std::vector. - Since a vector is only a 1D array, our storage will have to be a vector of vectors.
- std::vector is a template class. We can specify what data type it holds. e.g.
std::vector<int> arrayOfInts; - We want our vector to hold vectors that hold generic "T" data types. If you don't follow this, you need to stop and ask you TA for an explanation.
Assignment
- Define the instance variable(s) for the matrix template class.
- Write three methods for the matrix template class:
const matrix<T> &operator+=(const T &rhs)
- Adds the scalar value (of generic type T) to each element in this matrix<T>.
- Since this is a +=, you are changing the state of this object (e.g.
changing the vector of vectors). Therefore, this method is a mutator method.
- Return a constant reference to this.
matrix<T> operator*(const matrix<T> &rhs) const
- Multiplies this by the passed in matrix<T>.
- This is a constant method. You are NOT changing the state (instance variables) of this.
- Make a local matrix<T> object to perform the multiplication on.
- Return a copy of the local matrix<T> object.
- Matrix multiplication algorithm:
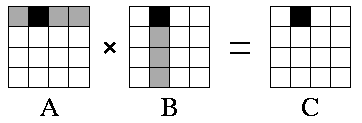
- For each row "row" in matrix A
- For each column "col" in matrix B
- Take the first element in row in A and multiply it by the first element in col in B.
- Take the second element in row in A and multiply it by the second element in col in B.
- Continue through all the elements.
- Add the products together.
- Put the result in the output matrix at row row, column col.
- Mechanics
- You will need one for loop for rows, one for columns, and one to loop through the multiplication
of the elements.
- You need to keep a running total of the products of the multiplications.
- You do not need temporary variables, other than the local matrix<T> object. (You may use
them though.)
- You need only one line inside the for loops to do the multiplication.
(Of course, you are allowed to have more.)
matrix<T> transpose () const
- Takes each element at [i][j] and puts it at [j][i].
- You can assume that the matrix is square (the number of rows equals the number columns).
- This is a constant method, so the state of this does not change.
- Make a local matrix<T> object to hold the result.
- Return a copy of the local matrix<T> object.
- Test your code with the driver class. NOTE: be sure to specify the data type to
be used with the matrix.
Starter Code
// forward declarations
template <typename T> class matrix;
template <typename T> std::ostream &operator<<(std::ostream &out, const matrix<T> &rhs);
template <typename T>
class matrix {
private:
// a vector of vectors (like an array of arrays)
// NOTE: Always put a space between 2 > (e.g. > >).
// Otherwise it looks like the input operator
______________________________ twoDArray;
public:
matrix (int row=4, int col=4);
// constant and non constant [] access to the matrix is provided
const std::vector<T> &operator[](int row) const { return twoDArray[row]; }
std::vector<T> &operator[](int row) { return twoDArray[row]; }
int rows () const { return twoDArray.size(); }
int cols () const { return rows() ? twoDArray[0].size() : 0; }
const matrix<T> &operator+=(const T &rhs);
matrix<T> operator*(const matrix<T> &rhs) const;
matrix<T> transpose () const;
friend std::ostream &(::operator<< <>)(std::ostream &out, const matrix<T> &rhs);
};
template<typename T>
matrix<T>::matrix<T> (int row, int col) : twoDArray(row) {
for (int i=0; i < row; ++i) {
twoDArray[i].resize (col);
}
}
template<typename T>
std::ostream &operator<< (std::ostream &out, const matrix<T> &rhs) {
out.setf (std::ios::fixed, std::ios::floatfield);
out.precision (2);
for (int i=0; i < rhs.rows(); ++i) {
out << "[";
for (int j=0; j < rhs.cols(); ++j) {
out.width(6);
j == rhs.cols()-1 ? out << rhs[i][j] : out << rhs[i][j] << ", ";
}
out << "]" << std::endl;
}
return out;
}
// Driver
#include "matrix.h"
template class matrix<float>;
template std::ostream &operator<< (std::ostream &out, const matrix<float> &m);
int main (int argc, char *argv[]) {
matrix<float> m1;
for (int i=0; i < m1.rows(); ++i) {
for (int j=0; j < m1.cols(); ++j) {
m1[i][j] = i * 4 + j;
}
}
std::cout << m1 << std::endl;
std::cout << "matrix: " << std::endl;
matrix<float> m2 = m1.transpose();
std::cout << "Transposed matrix: " << std::endl;
std::cout << m2 << std::endl;
matrix<float> m3 = m1 * m2;
std::cout << "matrix * transposed matrix: " << std::endl;
std::cout << m3 << std::endl;
m1 += 10;
std::cout << "matrix + 10: " << std::endl;
std::cout << m1 << std::endl;
}
const matrix<T> &operator+=(const T &rhs)
- Adds the scalar value (of generic type T) to each element in this matrix<T>.
- Since this is a +=, you are changing the state of this object (e.g. changing the vector of vectors). Therefore, this method is a mutator method.
- Return a constant reference to this.
matrix<T> operator*(const matrix<T> &rhs) const
- Multiplies this by the passed in matrix<T>.
- This is a constant method. You are NOT changing the state (instance variables) of this.
- Make a local matrix<T> object to perform the multiplication on.
- Return a copy of the local matrix<T> object.
- Matrix multiplication algorithm:
- For each row "row" in matrix A
- For each column "col" in matrix B
- Take the first element in row in A and multiply it by the first element in col in B.
- Take the second element in row in A and multiply it by the second element in col in B.
- Continue through all the elements.
- Add the products together.
- Put the result in the output matrix at row row, column col.
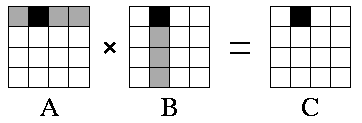
- Mechanics
- You will need one for loop for rows, one for columns, and one to loop through the multiplication of the elements.
- You need to keep a running total of the products of the multiplications.
- You do not need temporary variables, other than the local matrix<T> object. (You may use them though.)
- You need only one line inside the for loops to do the multiplication. (Of course, you are allowed to have more.)
matrix<T> transpose () const- Takes each element at [i][j] and puts it at [j][i].
- You can assume that the matrix is square (the number of rows equals the number columns).
- This is a constant method, so the state of this does not change.
- Make a local matrix<T> object to hold the result.
- Return a copy of the local matrix<T> object.
template <typename T> class matrix;
template <typename T> std::ostream &operator<<(std::ostream &out, const matrix<T> &rhs);
template <typename T>
class matrix {
private:
// a vector of vectors (like an array of arrays)
// NOTE: Always put a space between 2 > (e.g. > >).
// Otherwise it looks like the input operator
______________________________ twoDArray;
public:
matrix (int row=4, int col=4);
// constant and non constant [] access to the matrix is provided
const std::vector<T> &operator[](int row) const { return twoDArray[row]; }
std::vector<T> &operator[](int row) { return twoDArray[row]; }
int rows () const { return twoDArray.size(); }
int cols () const { return rows() ? twoDArray[0].size() : 0; }
const matrix<T> &operator+=(const T &rhs);
matrix<T> operator*(const matrix<T> &rhs) const;
matrix<T> transpose () const;
friend std::ostream &(::operator<< <>)(std::ostream &out, const matrix<T> &rhs);
};
template<typename T>
matrix<T>::matrix<T> (int row, int col) : twoDArray(row) {
for (int i=0; i < row; ++i) {
twoDArray[i].resize (col);
}
}
template<typename T>
std::ostream &operator<< (std::ostream &out, const matrix<T> &rhs) {
out.setf (std::ios::fixed, std::ios::floatfield);
out.precision (2);
for (int i=0; i < rhs.rows(); ++i) {
out << "[";
for (int j=0; j < rhs.cols(); ++j) {
out.width(6);
j == rhs.cols()-1 ? out << rhs[i][j] : out << rhs[i][j] << ", ";
}
out << "]" << std::endl;
}
return out;
}
// Driver
#include "matrix.h"
template class matrix<float>;
template std::ostream &operator<< (std::ostream &out, const matrix<float> &m);
int main (int argc, char *argv[]) {
matrix<float> m1;
for (int i=0; i < m1.rows(); ++i) {
for (int j=0; j < m1.cols(); ++j) {
m1[i][j] = i * 4 + j;
}
}
std::cout << m1 << std::endl;
std::cout << "matrix: " << std::endl;
matrix<float> m2 = m1.transpose();
std::cout << "Transposed matrix: " << std::endl;
std::cout << m2 << std::endl;
matrix<float> m3 = m1 * m2;
std::cout << "matrix * transposed matrix: " << std::endl;
std::cout << m3 << std::endl;
m1 += 10;
std::cout << "matrix + 10: " << std::endl;
std::cout << m1 << std::endl;
}
a.out.Use
sendlab.212.302 3 *.cpp *.h Makefile