Lab 12: Shortest Path: Dijkstra's Algorithm

Background

Graphs p. 339

Definitions

• A graph G=(V, E) consists of a set of vertices, V, and a set of edges, E.
• Each edge (a.k.a. arc) is a pair (v, w) where v, w ∈ V. If the pair is ordered, then the graph is a directed graph (a.k.a. digraph).
• A vertex w is adjacent to v if and only if (v, w) ∈ E.
• An edge may have an assigned weight or cost.
• A path in a graph is a sequence of vertices w₁, w₂, ... , w_N such that (w_i, w_i+1) ∈ E for 1 <= i < N. The length of the path is the number of edges or N-1.
• A cycle in a directed graph is a path of length at least 1 such that w₁=w_N.
• A directed graph is acyclic is it has no cycles. Such a graph is called a directed acyclic graphic or a DAG.
• An undirected graph is connected if there is a path from every vertex to every other vertex.
• A directed graph with this property is called strongly connected. If the directed would be considered connected if it were not directed, it is called weakly connected.
• A complete graph is a graph in which there is an edge between every pair of vertices.

Representations of Graphs

1. Adjacency matrix: a 2D array of boolean values. If there is an edge (u, v), then element [u][v] is true. If it is a weighted graph, then the matrix will hold the weights of the edges instead of boolean values. Unfortunately, the adjacency matrix requires |V|² space to store the graph. If the graph has only a few edges, this is expensive.
2. Adjacency list: For each vertex, we keep a (linked) list of the vertices adjacent to it. Each node of the linked list holds an identifier for the adjacent vertex and a weight. This representation requires only |V|+|E| space, which is considered linear for a graph.

Single-Source Shortest-Path Problem

• Supposed we have a graph with weighted edges and we wish to find the cheapest/shortest way from our starting vertex to every other vertex in the graph. This problem is called the shortest-path problem.
• Example applications of the shortest-path problem include computer networks and transportation routes.
• Problem Statement: Given as input a weighted graph, G=(V, E), and a distinguished vertex, s, find the shortest weighted path from s to every other vertex in G.
• For simplicity, we will assume that all weights are positive.

Assignment

1. Using C++ STL's priority_queue to represent a min heap and the map to represent graphs, implement Dijkstra's shortest path algorithm and test it on the directed graph given in the text (reproduced here for convenience).

   

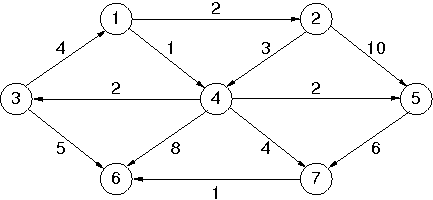
   Sample output (should match what's in the text):
   

   Dijkstra's from v1:
     to v1 costs 0 via 
     to v2 costs 2 via v1
     to v3 costs 3 via v4
     to v4 costs 1 via v1
     to v5 costs 3 via v4
     to v6 costs 6 via v7
     to v7 costs 5 via v4
   	

2. Using C++ STL's priority_queue and map to represent graphs, implement Prim's minimum spanning tree algorithm and test it on the graph given in the text (reproduced here for convenience, note the different weight of edge (v₄,v₅)).

   

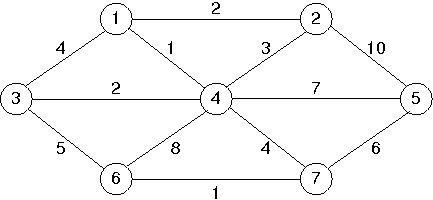
   Sample output (should match what's in the text):
   

   Prim's from v1:
     to v1 costs 0 via 
     to v2 costs 2 via v1
     to v3 costs 2 via v4
     to v4 costs 1 via v1
     to v5 costs 6 via v7
     to v6 costs 1 via v7
     to v7 costs 4 via v4
   	

Suggestions

1. Represent a vertex by a node_t class containing a string id with an int cost as well as a string predecessor. Make sure you have operator<, operator>, and operator== defined so that you can place verteces on the priority queue.

2. Represent the graph by a map mapping verteces into "adjacency sets" which are also stored as maps so that a directed graph is a map of maps using standard STL containers, e.g.,
   

   map<string,map<string,int> > graph;
   	

3. The STL priority_queue holds graph verteces ordered by increasing cost—use a min heap instead of the default max heap by declaring priority_queue with the greater<> comparator, e.g.,
   

   priority_queue<node_t,std::vector<node_t>,greater<node_t> > queue;
   	

4. Dijkstra's and Prim's methods (which are almost identical) should calculate the lengths of the shortest paths (or edges) from a start vertex to all other verteces and store this information in a separate map for costs, e.g.,
   

   map<string,int>    costs;
   	

5. Calculate paths by storing the "predecessor" of each vertex in (yet) another map—whenever a shorter route to a vertex is found the vertex the edge comes from is stored in this map, e.g.,
   

   map<string,string> paths;
   	

Turn in

1. A README file containing
   1. Course id--section no
   2. Name
   3. Lab description
   4. Brief solution description (e.g., program design, description of algorithm, etc., however appropriate).
   5. Lessons learned, identified interesting features of your program
   6. Any special usage instructions
2. Makefile
3. source code (.h headers and .cpp source)
4. object code (do a make clean before tar)

How to hand in