priority_queue to represent a
min heap and the map to represent graphs,
implement Dijkstra's shortest path algorithm and test it
on the directed graph given in the text
(reproduced here for convenience).
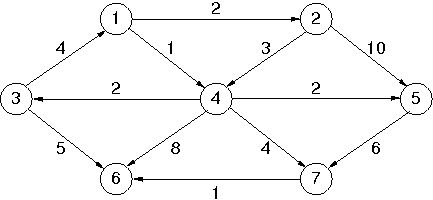
Sample output (should match what's in the text):
Dijkstra's from v1:
to v1 costs 0 via
to v2 costs 2 via v1
to v3 costs 3 via v4
to v4 costs 1 via v1
to v5 costs 3 via v4
to v6 costs 6 via v7
to v7 costs 5 via v4
priority_queue and map
to represent graphs, implement Prim's minimum spanning tree
algorithm and test it on the graph given in the
text (reproduced here for convenience, note the different
weight of edge (v4,v5)).
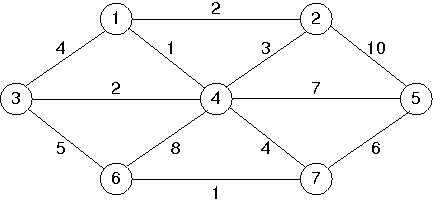
Sample output (should match what's in the text):
Prim's from v1:
to v1 costs 0 via
to v2 costs 2 via v1
to v3 costs 2 via v4
to v4 costs 1 via v1
to v5 costs 6 via v7
to v6 costs 1 via v7
to v7 costs 4 via v4