CPSC 212-002 Computer Science IV
(Data Structures and Algorithms)
Fall 2009
15:30-16:45TTH Daniel 415
Assignment 5

Objectives:
To implement Dijkstra's and Prim's algorithms

Due date:
10/29/09

What to hand in:
A tar.gz archive of your asg4/ directory, including:
  1. A README file containing
    1. Course id--section no
    2. Name
    3. Assignment description
    4. Brief solution description (e.g., program design, description of algorithm, etc., however appropriate).
    5. Lessons learned, identified interesting features of your program
    6. Any special usage instructions
  2. Makefile
  3. source code (.h headers and .cpp source)
  4. object code (do a make clean before tar)
How to hand in:
See handin notes

Description:
  1. Using C++ STL's priority_queue to represent a min heap and the map to represent graphs, implement Dijkstra's shortest path algorithm and test it on the directed graph given in the text (reproduced here for convenience).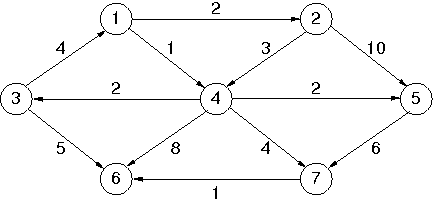

    Sample output (should match what's in the text):

    Dijkstra's from v1:
  to v1 costs 0 via 
  to v2 costs 2 via v1
  to v3 costs 3 via v4
  to v4 costs 1 via v1
  to v5 costs 3 via v4
  to v6 costs 6 via v7
  to v7 costs 5 via v4
  2. Using C++ STL's priority_queue and map to represent graphs, implement Prim's minimum spanning tree algorithm and test it on the graph given in the text (reproduced here for convenience, note the different weight of edge (v4,v5)).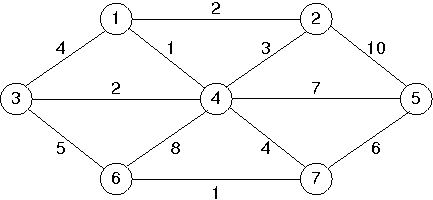

    Sample output (should match what's in the text):

    Prim's from v1:
  to v1 costs 0 via 
  to v2 costs 2 via v1
  to v3 costs 2 via v4
  to v4 costs 1 via v1
  to v5 costs 6 via v7
  to v6 costs 1 via v7
  to v7 costs 4 via v4
Suggestions:
  1. Represent a vertex by a Node class containing a string id with an int cost as well as a string predecessor. Make sure you have operator<, operator>, and operator== defined so that you can place verteces on the priority queue.

  2. Represent the graph by a map mapping verteces into "adjacency sets" which are also stored as maps so that a directed graph is a map of maps using standard STL containers, e.g.,
    map<string,map<string,int> > graph;
  3. The STL priority_queue holds graph verteces ordered by increasing cost—use a min heap instead of the default max heap by declaring priority_queue with the greater<> comparator, e.g.,
    priority_queue<Node,std::vector<Node>,greater<Node> > queue;
  4. Dijkstra's and Prim's methods (which are almost identical) should calculate the lengths of the shortest paths (or edges) from a start vertex to all other verteces and store this information in a separate map for costs, e.g.,
    map<string,int>    costs;
  5. Calculate paths by storing the "predecessor" of each vertex in (yet) another map—whenever a shorter route to a vertex is found the vertex the edge comes from is stored in this map, e.g.,
    map<string,string> paths;